- Collect a set of ranked ballots
- 18 voters distribute their ballots in the following manner:
- 7:a>b>c
- 5:b>a>c
- 4:c>a>b
- 2:b>c>a
- Based on a set of ranked ballots, compute the Pairwise Matrix
- 7:a>b>c has the equivalent Pairwise Matrix of:
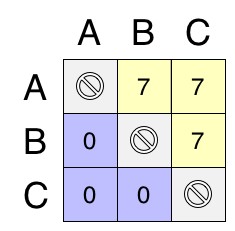
- 5:b>a>c has the equivalent Pairwise Matrix of:
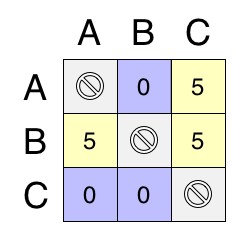
- 4:c>a>b has the equivalent Pairwise Matrix of:
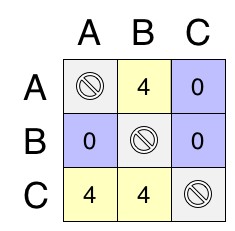
- 2:b>c>a has the equivalent Pairwise Matrix of:
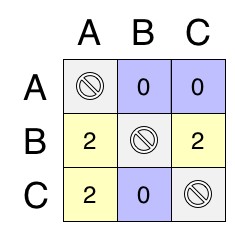
- The complete Pairwise Matrix (computed by adding the above four together) is:
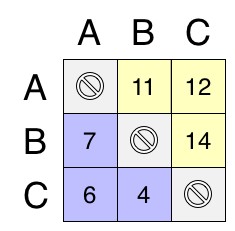
- Extract each of the defeats from the Pairwise Matrix
- The defeats are:
- A>B Strength:11 Margin:4
- A>C Strength:12 Margin:6
- B>C Strength:14 Margin:10
- Sort the defeats from strongest to weakest
- The sorted defeats are:
- B>C Strength:14 Margin:10
- A>C Strength:12 Margin:6
- A>B Strength:11 Margin:4
- Starting with the strongest defeat, consider each defeat in
sequence with previously kept defeats, if any. If two or
more defeats are equivalent, those defeats are considered
together with previously kept defeats, if any. If any defeat
under consideration, which has not yet been kept, is a part of a cycle,
it is rejected. If any defeat under consideration, which has not yet been kept,
is not a part of a cycle, it is kept.
- Consider the defeat B>C with our previously kept defeats.
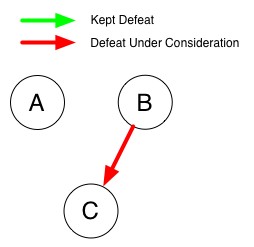
- No cycles are created, so it kept and we consider A>C with our previously kept defeats.
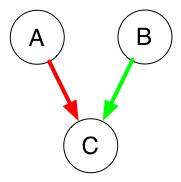
- No cycles are created, so it is kept and we consider A>B with our previously kept defeats.
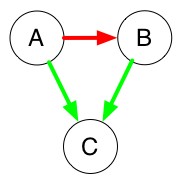
- No cycles are created, so it is kept.
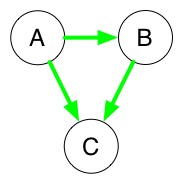
- The winner or winners will be those alternatives which were not defeated
- Since A is the alternative, after all defeats have been considered, to remain undefeated, it wins.
Back to Method Description
Back to the voting calculator








